Villas, Cars, and Interest Rates

The past several classes with Alec, Lukas, and Max, we've been talking about interest rates and about how much things really cost. If you want to buy a car, or a house, and you were to take out a loan, how much would you end up having to pay back? Of course, this has been drastically oversimplified so none of us get headaches.

Last week they were enjoying being "Unfair Banks" where they charged 99% interest on loans. Not realistic, but funny.

Since they were enjoying talking about large amounts of money last week, today we got really expensive. We pulled out the computers and by searching for "big fancy mansion," Lukas found a website selling French Villas. Things are expensive in the south of France - the one they wanted to buy cost 27,500,000 Euros. Yes, you read that correctly.

We pulled out the currency converter and found that this comes to roughly $37 million in US currency. We searched for current interest rates on house loans and found one that was 4.75% interest. Dividing by 365, the daily interest rate would be roughly .013%.

If you took out a $37 million loan to buy this house, ONE DAY of interest would cost you approximately

(.00013)(37,000,000)=$4810.

That's enough to buy a car. Probably a used car, but still a car.

Probability and Falling Down

On Thursday we explored probability using ideas I got from a UMS workshop with Dr. Schaffer and Mr. Stern, founders of Math Dance.

First we warmed up by doing things like "make a shape with two hands on the floor but no feet."

We progressed from shapes to movements. Everyone had to make up a movement, which could be pretty much anything so long as it had a beginning and an end and didn't involve running into furniture or people. Several kids chose to fall down, because, hey, falling down is fun!

We voted on which movements we liked the best and settled on two: Lydia's, which involved running around like a horse, and Daniel's, which involved spinning around and then falling down. Everyone learned both movements.

Then came the probability. We flipped a coin 5 times. Heads meant Daniel's movement, Tails meant Lydia's movement. We ended up with a 5-move dance, which we were doing as Renata walked through the room and wondered what on earth this had to do with math! Then we made up another dance by doing another set of coin flips. Then we flipped coins some more because everyone wanted a turn to be the coin flipper.

Although there was a lot of falling down, yes, we really were doing math!

• Problem-solving: How do you get two hands on the floor and no feet? How do you make these different shapes with your body?
• Probability: Instead of just seeing that the coin comes up about half heads and about half tails, there's a physical understanding that the coin tells you to do one move about half the time and the other move about half the time.
• Collaboration: How do we all run around like horses in a small room without crashing into each other?

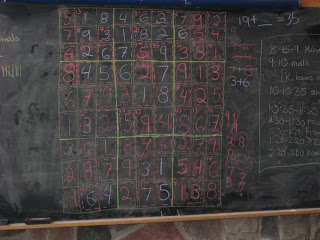
Today we concentrated on the coin-flipping aspect. Each kid flipped a coin 100 times and recorded the number of heads and tails. Most got about 45/55, one got 31/69, one got 50/50. Not everyone made it to 100 flips, but those that didn't still got about half one and half the other.

Everyone recognized 31/69 as being interesting, so we talked about what could have caused so many tails. The flipper of that coin suggested the head side was heavier. Someone else said that pennies are made like a sandwich, with a core of one metal inside and another metal on the outside, and suggested that the core of this coin could be off-center, which would mess with the balance.

Killer Sudoku, cont.

We finished the Killer Sudoku! Here it is, in all its glory:

And here's Saul posing with the finished puzzle:

Perimeter and City Blocks

At some point in your life you were probably asked a question like this: what is the perimeter of this shape?

This is known as a "composite" shape, and kids are taught to find the perimeter of such a thing by looking at it as a bunch of rectangles stuck together, finding the length of each little line, and then adding the lengths. This is a fine method, works great. However, when the shapes are particularly nice, there's a much easier way.

This easier way is based on how we measure distances in a city. Assuming we can't cut through buildings, we measure distances in a city by blocks. In the picture below, the distance from A to B is 7 blocks. Any reasonable path from A to B must go a total of 4 blocks East and 3 blocks North. We don't have to do all the traveling East at once - we might go 1 block E, then 3 blocks N, then 3 blocks E. We've still travelled a total of 4 blocks E and 3 blocks N.

This brings us back to the original question, how to find the perimeter of the composite shape. We can think of this shape as being made of two paths from A to B, where each path uses only the directions E and N.

Looking at the "lower" path, we see that to travel from A to B one must go a total of 24 blocks E and 15 blocks N. Although we aren't given any distances on the "upper" path, we know that the red line segments on the upper path must take us the same distance East as the red line segments on the lower path (24 blocks). Similarly, the black line segments on the upper path must take us the same distance North as the black line segments on the lower path (15 blocks).

The upper and lower path each go 24 blocks E and 15 blocks N, so the total perimeter is

2(24+15)=2(39)=78.

Warning: this trick is just for shapes made up of two paths that only travel East and North!

My first math publication!

About two years ago I submitted a paper to the journal "Discrete Mathematics." I got the response "revise and resubmit" (translation: "make some changes, then we'll look at it again"). I revised and resubmitted and got the same response. I revised and resubmitted. Last week, I got a different response: my paper has been accepted for publication!

The name of the paper is "Improved Upper Bounds for the Information Rates of the Secret Sharing Schemes Induced by the Vamos Matroid." There are very few people in the world who know exactly what that means.

To summarize the punchline, there's a number x that mathematicians know is less than 10/11 (about .91) and a number y that mathematicians know is less than 9/10 (.9). I showed that x has to be less than 8/9 (about .89) and y has to be less than 17/19 (about .895). This probably doesn't sound like a big deal, but it was a big enough deal for the paper to get accepted! A surprisingly large amount of math consists of chipping away at numbers like this.

My favorite part is the way I showed that x and y had to be smaller than previously thought. Instead of using equations, I found a way to prove things using pretty pictures. :)

Killer Sudoku

"Killer Sudoku" is like normal sudoku but with a twist. Instead of being given some numbers to start with, you're told what certain groups of cells add up to. For example, if you know that the numbers in two cells must add up to 17, you know the number in one cell must be 8 and the other must be 9 (although you don't know which number goes in which cell).

Today we started work on this puzzle. The kids felt like it was going very slowly because we weren't able to fill in many numbers, but they were making great progress at narrowing down the options, which is how it goes with these puzzles!

A General Thank-You

Thank you to all the families who chipped in for the gift card! I'm having fun deciding how best to use it at Bellanina. :)

I hope everyone had a nice holiday season, and wish you all the best for 2011!

Jesse

Coloring

New year, new math. I'm tired of origami (the three-headed dragon took a very long time), so we're moving on.

Right now we're working on coloring "maps." The "maps" are drawings with various shapes, and each shape is considered its own country - no funny stuff like Alaska not being attached to the rest of the US.

When coloring, two countries that share a border aren't allowed to be the same color. If two countries only touch at a corner (like Utah and New Mexico in the 4 corners), they are not considered to share a border, so they are allowed to be the same color.

The challenge: given a map, how many colors do you need to be able to color it following the rules? Use the smallest number of colors you can get away with.

Here's an example:

We can't color this following the rules with only 1 color, or with 2. What about 3? Maybe we need 4, or 5.

I gave the kids a bunch of maps (this was the hardest one) and for each map they figured out the smallest number of colors they could get away with. Then they drew their own maps and started figuring out how many colors they would need for those.